最近学习吴恩达《Machine Learning》课程以及《深度学习入门:基于Python的理论与实现》书,一些东西总结了下。现就后者学习进行笔记总结。本文是本书的学习笔记(三)神经网络。
感知机优缺点:
- 即便对于复杂的函数,感知机也隐含着能够表示它的可能性。
- 但设定权重的工作,即确定合适的、能符合预期的输入与输出的权重,现在还是由人工进行的。
而神经网络的出现就是为了解决上面设定权重工作的缺点的。神经网络的可以自动地从数据中学习到合适的权重参数。
激活函数
将输入信号的总和转换为输出信号,这种函数一般称为激活函数。激活函数决定如何来激活输入信号的总和。激活函数是连接感知机和神经网络的桥梁。
感知机中使用了阶跃函数(一旦输入超过阈值,就切换输出的函数)作为激活函数。
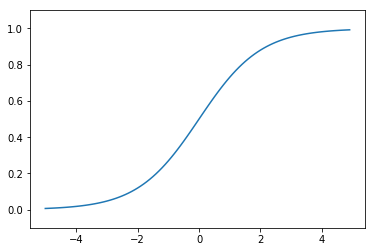
sigmoid函数
$$h(x)=\frac{1}{1+exp(-x)}$$
import numpy as np
import matplotlib.pylab as plt
#实现简单的阶跃函数
def step_function0(x):
if x > 0:
return 1
else:
return 0
def step_function1(x):
y = x >0
return y.astype(np.int)
def step_function(x):
return np.array(x > 0, dtype=np.int)
x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()
#sigmoid函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
yy = sigmoid(x)
plt.plot(x,yy)
plt.ylim(-0.1,1.1)
plt.show()
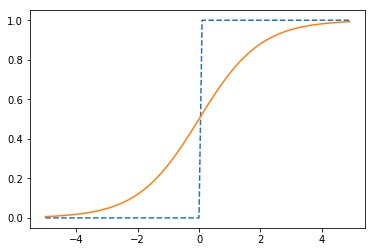
plt.plot(x,y,linestyle = "--",label="step")
plt.plot(x,yy,label="sigmoid")
plt.show()
可以看出,感知机中神经元之间流动的是0或1的二元信号,而神经网络中流动的是连续的实数值信号。
简单总结如下:
- sigmoid函数具有平滑性。
- 两个函数结构均是“输入小时,输出接近0或为0,随着输入增大,输出趋向于1或变为1”,也就是说,当输入信号为重要信息时,阶跃函数和sigmoid函数都会输出较大的值;当输入信号为不重要的信息时,两者都输出较小的值。
- 不管输入信号多大多小,输出信号值范围在0-1之间。
- 两者均为非线性函数。
**神经网络的激活函数必须使用非线性函数。**若使用线性函数,加神经网络是没有意义的。线性函数的问题是不管如何加深层数,总是存在与之等效的“无隐藏层的神经网络”。
举例:若将线性函数$h(x)=cx$作为激活函数,把$y(x)=h(h(h(x)))$的运算对应3层神经网络,这个运算会进行$y(x)=c\times c\times c\times x$的乘法运算,但是同样的处理可以由$y(x)=ax$这一次的乘法运算(即没有隐藏层的神经网络)来表示。注意这里$a=c^{3}$。
ReLU函数
在神经网络的发展史上,sigmoid函数很早就开始使用了,而最近则主要使用ReLU(Rectified Linear Unit)函数。
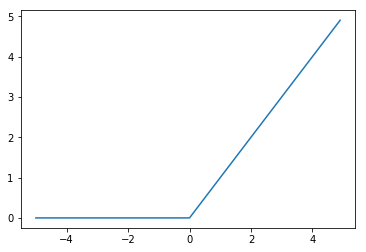
ReLU函数是一个非常简单的函数。ReLU函数在输入大于0时,直接输出该值;在输入小于0时,输出0。ReLU函数可以表示为下面的式子:
$$
h(x)=\begin{cases}
x&(x>0) \ 0&(x\leq 0)
\end{cases}
$$
#ReLU函数实现
def relu(x):
return np.maximum(0,x)
y3 = relu(x)
plt.plot(x,y3)
plt.show()
多维数组的运算
# 一维数组
import numpy as np
A = np.array([1, 2, 3, 4])
print(A)
[1 2 3 4]
np.ndim(A)#获取数组维数
1
A.shape#获取数组的形状
(4,)
A.shape[0]#其结果是个元组(tuple)
4
# 二维数组,也是矩阵
B = np.array([[1,2], [3,4], [5,6]])
print(B)
[[1 2]
[3 4]
[5 6]]
np.ndim(B)
2
B.shape
(3, 2)
# 矩阵乘法
C = np.array([[1,2],[3,4]])
C.shape
(2, 2)
D = np.array([[5,6],[7,8]])
D.shape
(2, 2)
np.dot(C,D)#乘积为点积
array([[19, 22],
[43, 50]])
np.dot(D,C)#绝大部分矩阵不满足乘法交换律
array([[23, 34],
[31, 46]])
神经网络的内积
使用NumPy矩阵实现神经网络。
# 使用NumPy矩阵实现神经网络
X=np.array([1,2])
X.shape
(2,)
W=np.array([[1,3,5],[2,4,6]])
print(W)
[[1 3 5]
[2 4 6]]
W.shape
(2, 3)
YY=np.dot(X,W)
print(YY)
[ 5 11 17]
3层神经网络的实现
神经网络的运算可以作为矩阵运算打包进行。
任何前一层的偏置神经元“1”都只有一个。偏置权重的数量取决于后一层的神经元的数量(不包括后一层的偏置神经元“1”)。
# 多维数组实现A(1)=XW(1)+B
# 输入层到第1层的信号传递
X=np.array([1.0, 0.5])
W1=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1=np.array([0.1,0.2,0.3])
print(W1.shape)
print(X.shape)
print(B1.shape)
(2, 3)
(2,)
(3,)
A1=np.dot(X,W1)+B1
#观察第1层中激活函数的计算过程,激活函数使用sigmoid
Z1=sigmoid(A1)
print(A1)
print(Z1)
[0.3 0.7 1.1]
[0.57444252 0.66818777 0.75026011]
#第1层到第2层的信号传递
W2=np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
B2=np.array([0.1,0.2])
print(Z1.shape)
print(W2.shape)
print(B2.shape)
A2=np.dot(Z1,W2) + B2
Z2=sigmoid(A2)
(3,)
(3, 2)
(2,)
#第2层到输出层的信号传递
#定义输出层的激活函数为恒等函数
def identity_function(x):
return x
W3=np.array([[0.1,0.3],[0.2,0.4]])
B3=np.array([0.1,0.2])
A3=np.dot(Z2,W3)+B3
Y=identity_function(A3)
print(Y)
[0.31682708 0.69627909]
输出层所用的激活函数,要根据求解问题的性质决定。一般地,回归问题可以使用恒等函数,二元分类问题可以使用sigmoid函数,多元分类问题可以使用softmax函数。
代码实现小结
# 3层网络实现案例,把权重记为大写字母W1,其他的偏置或中间结果等用小写字母表示
def init_network():
network = {}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3])
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])
network['b3'] = np.array([0.1,0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)
[0.31682708 0.69627909]
这里定义了init_network()和forward()函数。init_network()函数会进行权重和偏置的初始化,并将它们保存在字典变量network中。这个字典变量中保存了每一层所需的参数(权重和偏置)。forward()函数中则封装了将输入信号转换为输出信号的处理过程。
输出层的设计
神经网络可以用在分类问题和回归问题上,不过需要根据情况改变输出层的激活函数。一般而言,回归问题用恒等函数,分类问题用softrmax函数。
恒等函数和softmax函数
恒等函数会讲输入按原样输出,对于输入的信息,不加以任何改动地直接输出。
分类问题中使用的softmax函数可以用下面式子表示:
$$y_{k}=\frac{exp(a_{k})}{\sum_{i=1}^{n}exp(a_{i})}$$
$exp(x)=e^x$。上式表示假设输出层共有$m$个神经元,计算第$k$个神经元的输出$y_{k}$。softmax函数的分子是输入信号$a_{k}$的指数函数,分母是所有输入信号的指数函数的和。
从式中可看出,输出层的各个神经元都受到所有输入信号的影响。
实现softmax函数:
#实现softmax函数
a = np.array([0.3, 2.9, 4.0])
exp_a = np.exp(a) #指数函数
print(exp_a)
sum_exp_a = np.sum(exp_a) #指数函数的和
print(sum_exp_a)
y = exp_a / sum_exp_a
print(y)
[ 1.34985881 18.17414537 54.59815003]
74.1221542101633
[0.01821127 0.24519181 0.73659691]
# 定义softmax函数。供以后使用(初始版)
def softmax1(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
实现softmax函数时的注意事项
softmax实现需要注意溢出问题,因为softmax函数内有$exp(x)$的指数运算,会使数值变得很大。因此,softmax函数的实现可以按如下式改进:
$$
y_{k}=\frac{exp(a_{k})}{\sum_{i=1}^{n}exp(a_{i})}=\frac{C exp(a_{k})}{C \sum_{i=1}^{n}exp(a_{i})}=\frac{exp(a_{k}+log C)}{\sum_{i=1}^{n}exp(a_{i}+log C)}=\frac{exp(a_{k}+C^{'})}{\sum_{i=1}^{n}exp(a_{i}+C^{'})}
$$
在进行softmax的指数函数的运算时,加上或者减去某个常数并不会改变开运算的结果。这里的$C^{'}$可以使用任何值,但是为了防止溢出,一般会使用输入信号中的最大值。如下例:
# 演示计算溢出情况与解决
a = np.array([1010, 1000, 990])
np.exp(a) / np.sum(np.exp(a)) #softmax,并未正确被计算,报错
/opt/conda/lib/python3.6/site-packages/ipykernel_launcher.py:3: RuntimeWarning: overflow encountered in exp
This is separate from the ipykernel package so we can avoid doing imports until
/opt/conda/lib/python3.6/site-packages/ipykernel_launcher.py:3: RuntimeWarning: invalid value encountered in true_divide
This is separate from the ipykernel package so we can avoid doing imports until
array([nan, nan, nan])
c = np.max(a) #1010
a - c
np.exp(a - c) / np.sum(np.exp(a - c))
array([9.99954600e-01, 4.53978686e-05, 2.06106005e-09])
# 定义softmax函数。供以后使用(正式用版)
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c)#溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
softmax函数的特征
softmax函数的输出是0.0到1.0之间的实数。并且,softmax函数的输出值的总和是1.输出总和为1是softmax函数的一个重要特质,这个特质让softmax函数的输出解释为“概率”。通过softmax函数,我们可以用概率的(统计的)方法处理问题。
# 可解释为“概率”的softmax函数
a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)
np.sum(y)
[0.01821127 0.24519181 0.73659691]
1.0
上例中,从概率的结果来看,可以说“因为第2个元素的概率最高,所以答案是第2个类别”。而且,还可以回答“74%的概率是第2个类别,有25%的概率是第1个类别,有1%的概率是第0个类别”。
这里需要注意,即使使用了softmax函数,各个元素之间的大小关系也不会改变。这是因为指数函数是单调递增函数。
一般而言,神经网络只把输出值最大的神经元所对应的类别作为识别结果。并且,即使使用softmax函数,输出值最大的神经元的位置也不会改变。因此,神经网络在进行分类时,输出层的softmax函数可以省略。在实际问题中,由于指数函数的运算需要一定的计算机运算量,因此输出层的softmax函数一般会直接省略。
求解机器学习问题的步骤可以分为“学习”和“推理”两个阶段。首先,在学习阶段进行模型的学习(指使用训练数据、自动调整参数的过程),然后,在推理阶段,用学到的模型对未知的数据进行推理(分类)。如前所述,推理阶段一般会省略输出层的softmax函数。在输出层使用softmax函数是因为它和神经网络的学习有关系。
输出层的神经元数量
输出层的神经元数量需要根据待解决的问题来决定。对于分类问题,输出层的神经元数量一般设定为类别的数量。
手写数字识别
求解机器学习问题的步骤粉尘搞学习和推理两个阶段进行,和其一样,神经网络解决问题时,也需要首先使用训练数据(学习数据)进行权重参数的学习;进行推理时,使用刚才学习到的参数,对输入数据进行分类。
# 代码暂略
import sys, os
print(sys.path.append(os.pardir))
None